Dividing fractions using fraction strips: An evidence-based math strategy

Dividing fractions can be really tough for many students. It’s hard to visualize splitting a fraction up into groups of other fractions. To divide fractions, many students memorize the “keep-change-flip” algorithm without knowing why it works.  

Without a conceptual understanding of dividing fractions, students tend to get stuck when they come across problems (especially word problems) where they have to divide by non-unit fractions like 2/3 or 3/4, or problems where the divisor is larger than the dividend.

By sixth grade, when students need to divide mixed numbers, they often rely heavily on the multi-step “keep-change-flip” method that is hard to memorize and understand.  

You can help your students understand how to divide fractions by using fraction strips that they can move around. Manipulatives and visual representations are evidence-based strategies that support learning new math concepts. Fraction strips can help students not only understand the concept of dividing fractions, but literally see how to solve these problems without having to do any calculations. 

Download: Printable fraction strips

Read: How to use this strategy

Objective: Students will use fractions strips to show and solve the division of two fractions. 

Grade levels (with standards): 

• 5 (Common Core 5.NF.B.7: Apply and extend previous understandings of division to divide unit fractions by whole numbers and whole numbers by unit fractions)

• 5 (Common Core 5.NF.B.7.B: Interpret division of a whole number by a unit fraction, and compute such quotients)

• 6 (Common Core 6.NS.A.1: Interpret and compute quotients of fractions, and solve word problems involving division of fractions by fractions, e.g., by using visual fraction models and equations to represent the problem)

• 5–6 (Common Core Math Practice MP1: Make sense of problems and persevere in solving them; Common Core Math Practice MP5: Use appropriate tools strategically)

Best used for instruction with: 

• Whole class

• Small groups

• Individuals

How to prepare:

Gather and explore materials. Give each student or pair of students a set of fraction strips. Have students cut each strip into unit fractions (with a numerator of 1). For students who struggle with fine motor skills, consider having a few sets already cut out. You could also make a few laminated or card stock sets for students. 

After cutting each strip into unit fractions, have students reassemble each of the strips so they have a complete set that matches what’s in the printable. Give students a copy of the printable, or project an image of the printable so they have a visual model to refer to.     

Once students have all the strips arranged, reintroduce the concept of a whole. Remind students that the visual representation of 1 and the word “whole” are often interchangeable when we talk about fractions. Say, “At the top of our set we have 1 whole piece.” Then, ask students what they notice about the strips beneath the whole piece. Model an example. You could say, “I notice that each row of fractions strips is the same size.” Have students share what they notice with a partner. Then ask a few students to share with the entire class. Remind students of previous lessons where they worked on dividing whole numbers by fractions. 

How to teach:

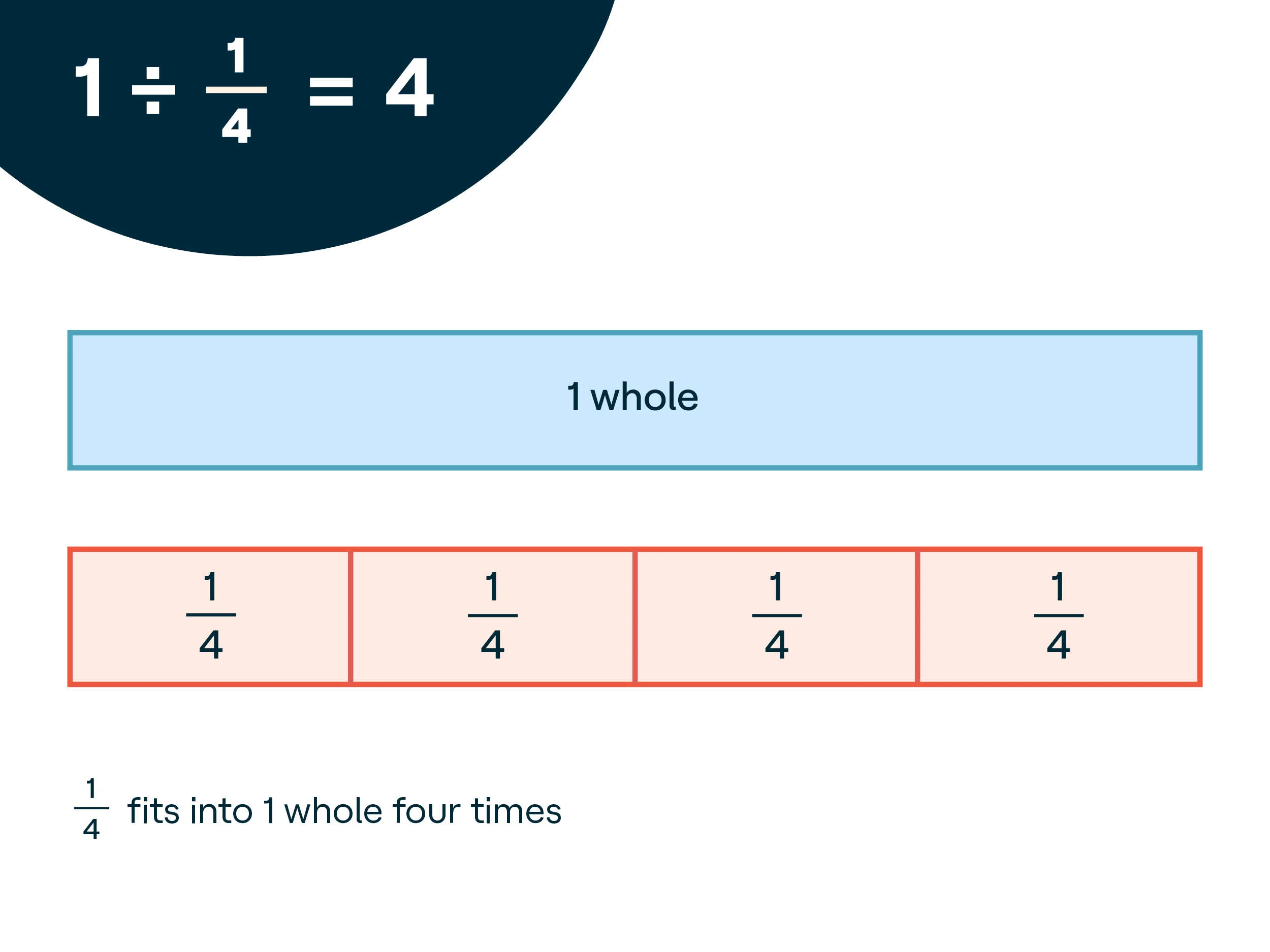
1. Review dividing a whole number by a fraction. Ask students to place the 1 whole strip at the top of their desk. Beneath that strip, have students place as many 1/4 strips as needed to match the same size as 1 whole. Write the equation 1 ÷ 1/4 = 4 on the board and ask the students how they know this is true.  Students should refer to the strips in front of them to explain the answer.

Review all the common ways students could explain their answers by providing the following examples both visually and verbally:  

• “1/4 fits into 1 whole 4 times” 

• “There are 4 groups of 1/4 in 1 whole” 

• “1 divided into groups of 1/4 is 4” 

• “4 times 1/4 equals 1”

2. Explain how to use fraction strips to divide a fraction by a fraction. Use the “I Do, We Do, You Do” model (also known as a gradual release model of instruction) to guide students through the process of using the strips.  

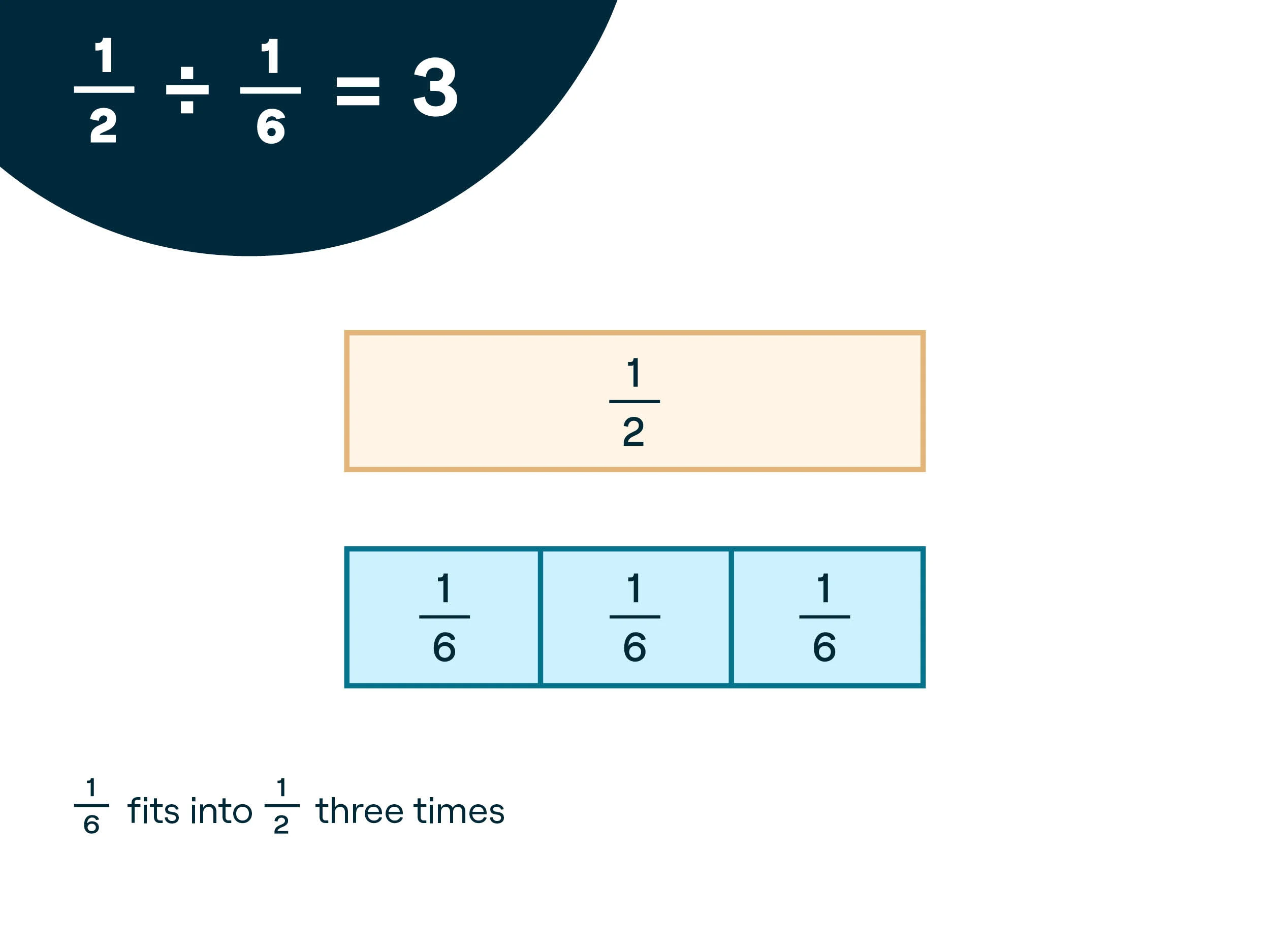
I Do: Explain and model using the strips. Say, “Now we can use a similar strategy to solve division problems with two fractions in them. Let’s take a look at 1/2 ÷ 1/6. I’ll start by placing a 1/2 strip at the top like this. Next, underneath it, I’ll put as many 1/6 strips as I can to match the 1/2 strip. We can see that it takes one, two, three 1/6 strips to match the 1/2 strip. So I can conclude that 1/2 ÷ 1/6 = 3, or 1/6 fits into 1/2 three times.”

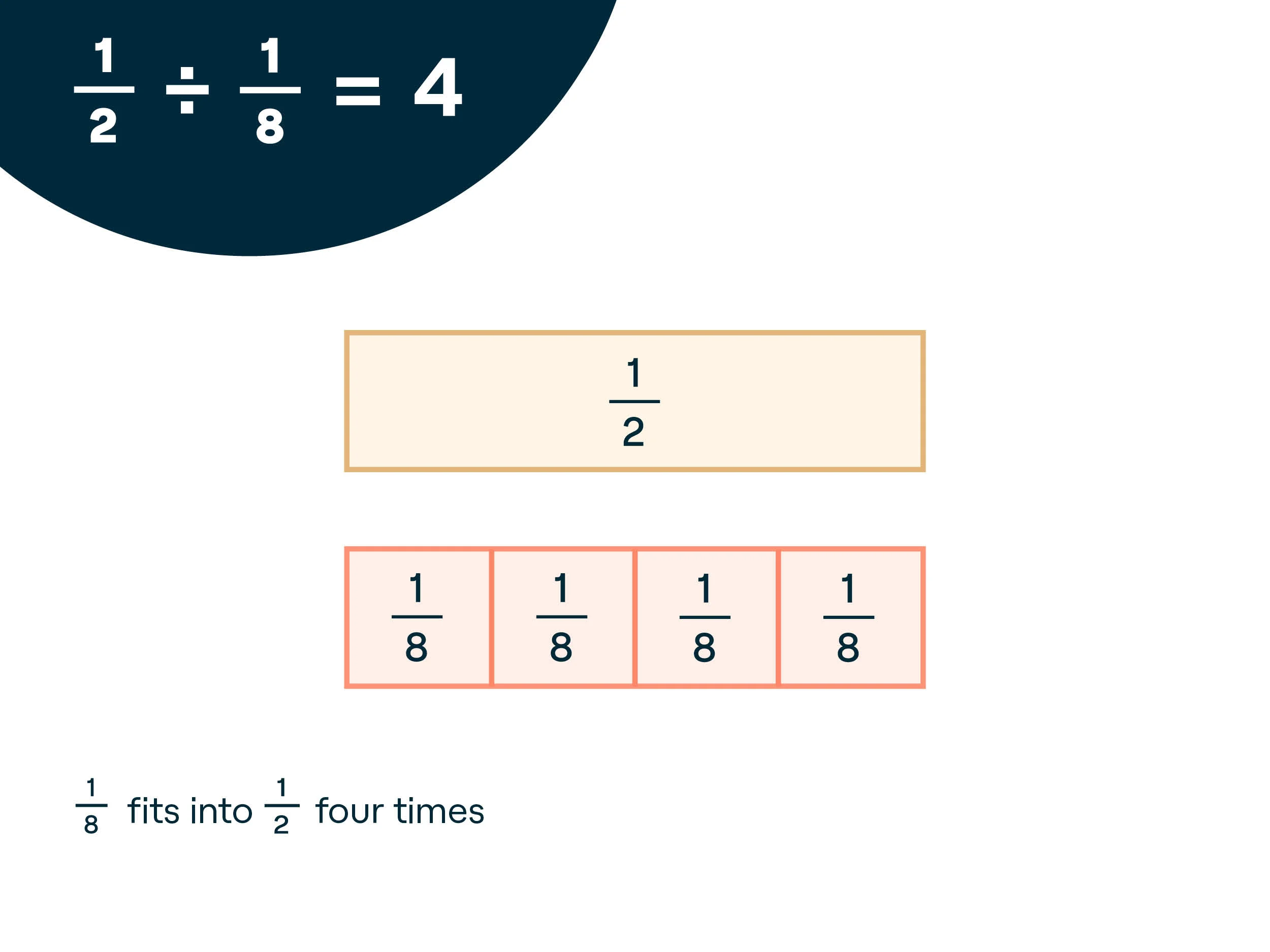
We Do: Guide students through trying it with you. Say, “Now let’s try this together. Start with 1/2 again. I will place 1/2 at the top. You do the same.” Model placing the 1/2 strip at the top. “This time divide 1/2 by 1/8. Let’s place as many 1/8 strips as we can to match the 1/2 strip.” Model it and then walk around to help students who may need support. For students who are able to set it up correctly, prompt them to write out the division problem with the solution. 

Once everyone has finished, discuss the answer as a class. Write the division number sentence for students who may not have gotten the correct answer. Describe the solution in multiple ways.

You Do: Choose three division problems using unit fractions for both the divisor and the dividend. Tell students they’ll be doing them on their own. Say, ”Try the next several problems by yourself or with your partner. Be sure to write the division sentence with your solution once you have set it up using your fractions strips.” Provide guidance as needed. When checking in, ask students to explain their solutions using the language discussed at the beginning of class, such as “____ groups of ____ fit into ____.”

Teaching tip: Many students, including English language learners (ELLs) and students who struggle with expressive language, benefit from having sentence frames at their desks. Print out a set of frames and put them in dry-erase pockets so students can write out their answers each time. 

3. Move on to practicing more challenging problems. Follow the “I Do, We Do, You Do” model again. 

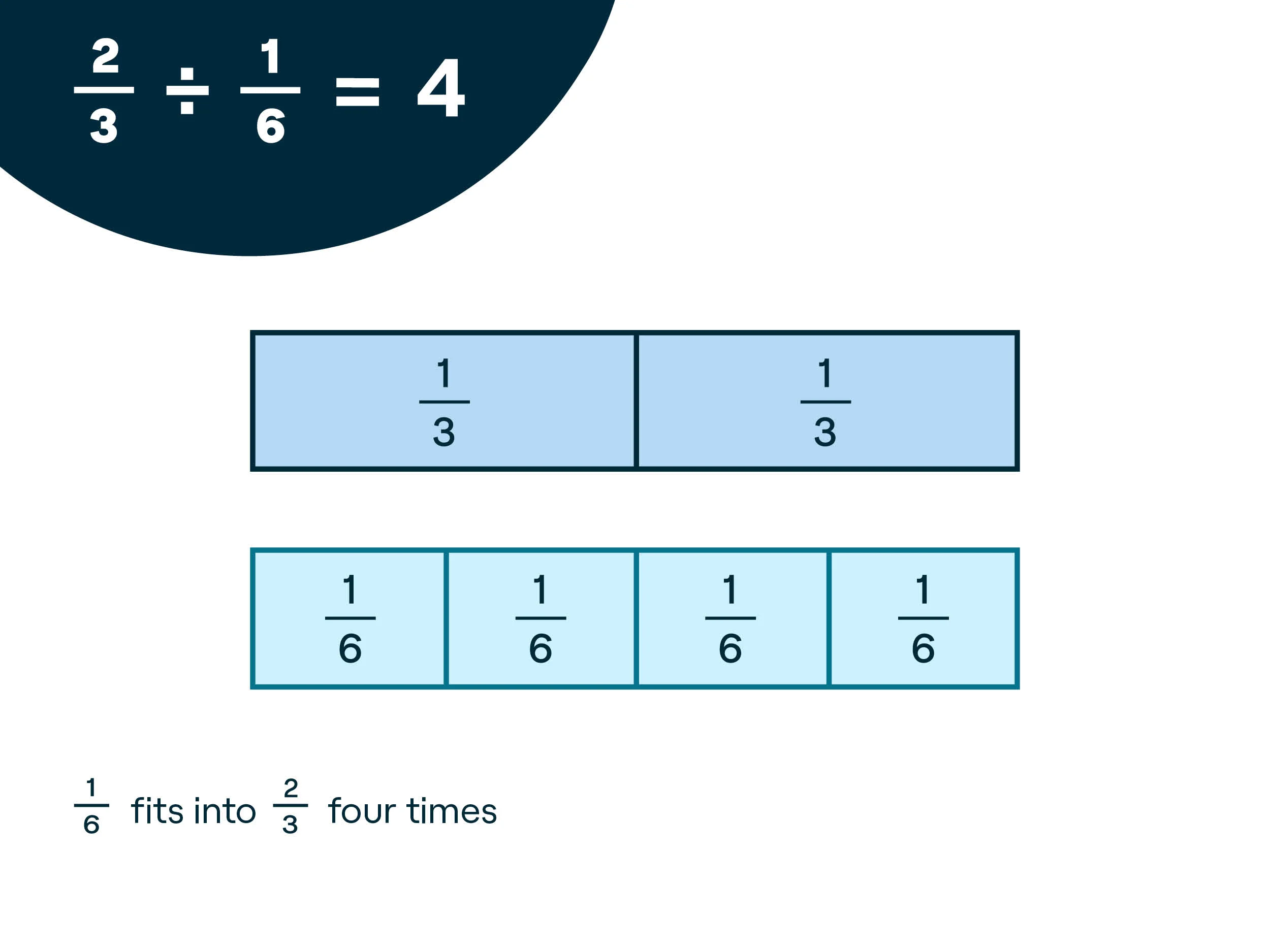
I Do: Say, “Let’s try some problems that are a little more challenging. This time begin with 2/3.” Model for them. Students should follow by placing two 1/3 strips at the top of their desk.  “I want you to divide 2/3 by 1/6.” Demonstrate how to line up 1/6 strips below 2/3 until you have matched the whole. Count the number of strips you used out loud while pointing them out. “So, 2/3 ÷ 1/6 = 4.”  

We Do: “Now, let’s do this next one together. Let’s try 3/4 ÷ 1/8. I’m going to show 3/4 at the top using three 1/4 strips. You do the same.” Model placing the 3/4 at the top. “This time, divide 3/4 by 1/8. Let’s place as many 1/8 strips as we can to match the 3/4 strip.” Model it and then walk around to help students who may need support. For students who are able to set it up correctly, prompt them to write out the division problem with the solution. 

Once everyone has finished, discuss the answer as a class. Write the division number sentence for students who may not have gotten the correct answer. Describe the solution in multiple ways.

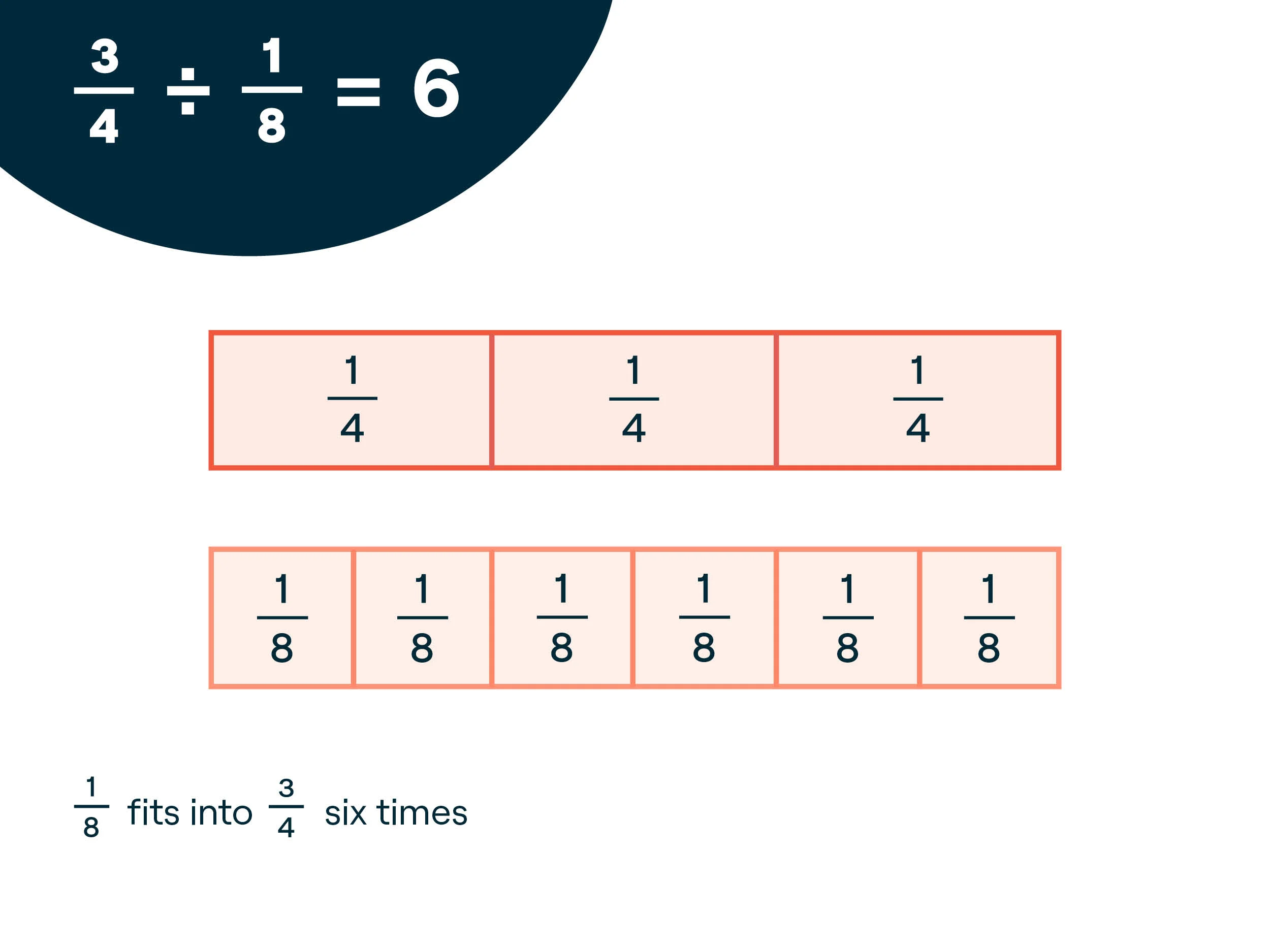
You Do: Provide several practice problems for students to try independently. Check in to see how students are using the fraction strips. Some students by this point may have figured out how to solve the problems without using the strips. Talk with these students about what procedure they are using. If you feel the class is ready at the end of the lesson, have these students demonstrate the keep-change-flip algorithm. This will help begin the transition to using the algorithm over the fraction strips. 

4. Continue to practice. Some students may begin to solve without the fraction strips. Others will continue to use them. As everyone practices, challenge the students who are using the strips to draw models for each division problem instead. They can refer back to the strips as a reference, but drawing their own versions of the strips will help transition from the concrete of strips to the abstract of numbers. 

Understand: Why fraction strips work

Fraction strips (or fraction bars or tiles) help students see that the same “whole” can be broken up into different equal-size parts. When students move the strips and put them side by side, they can visualize the fractional amounts. They can also make comparisons between fractions and do addition, subtraction, multiplication, and division with fractions.    

Students who experience difficulty with math, particularly with fractions, often have trouble connecting meaning to the numbers and symbols in an algorithm. Fraction strips give students a conceptual representation of the problem. They can use the strips to create both the dividend and the divisor so that they can see both as fractional parts of a whole. Students can also count the number of groups (the quotient) made by dividing. 

With this strategy, you use explicit instruction in the “I Do, We Do, You Do” model. By showing students how to use the fraction strips and then allowing them to practice with both teacher and peer support, this strategy provides multiple learning opportunities. 

Using this strategy before moving on to divisors that are not unit fractions will help students have a better understanding of why the algorithm works, not just how it works.  

Connect: Link school to home

Once students are familiar with how to use the fraction strips, send a new fraction strip page home or a set that has already been cut out. Families can help reinforce using fraction strips at home when students are working on their homework.

If you find families are confused by the homework, consider sending this resource to help parents and caregivers understand why math is taught differently now than when they were in school. 

Research behind this strategy

“The concrete-representational-abstract approach for students with learning disabilities: An evidence-based practice synthesis,” from Remedial and Special Education

“Explicit mathematics instruction: What teachers can do for teaching students with mathematics difficulties,” from Intervention in School and Clinic